Ludomir Wolfke (Warszawa), Podstawy geometrji wykreślnej

W referacie niniejszym miałem zamiar podać szereg spostrzeżeń, dotyczących tej podstawowej metody, odwzorowania, jaką stanowi metoda rzutu środkowego. Licząc się jednak z brakiem czasu i nie chcąc absorbować uwagi Sz. Panów zagadnieniami drugorzędnemi – posiadającemi wyłącznie charakter dydaktyczny – zmuszony jestem ograniczyć treść mego przemówienia do rzeczy najistotniejszych.

Nie będę przytaczać znanych argumentów, uzasadniających wyjątkowe znaczenie teorji rzutu środkowego i określających stosunek Geometrji rzutowej do Geometrji wykreślnej, gdyż sprawa ta została już dawno należycie oświetlona przez znanego reformatora Geometrji wykreślnej: Wilhelma Fiedlera. Wiemy również wszyscy o owocnej działalności prof. dr. Mieczysława Łazarskiego, który przez szereg lat reprezentował analogiczny kierunek na politechnice lwowskiej.

W obecnej chwili jednak, z łatwością stwierdzić możemy, że teoretyczne przeświadczenie o doniosłości metody rzutu środkowego uległo znacznemu osłabieniu. Jestem skłonny przypuszczać, że jedną z głównych przyczyn powyższego faktu są pewne trudności metodyczne w racjonalnem ustosunkowaniu Geometrji rzutowej do Geometrji wykreślnej.

W systematycznym wykładzie Geometrji rzutowej, teorja homologji (kolineacji perspektywicznej) stanowi część ogólnej teorji odpowiedniości jednokreślnych (homograﬁcznych). Urzeczywistnienie podobnego planu w wykładach Geometrji wykreślnej jest niewątpliwie połączone ze znacznemi trudnościami dydaktycznemi; sądzimy jednak, że narracyjne traktowanie teorji homologji – ujawniające zupełną rezygnację z należytego uzasadnienia tak podstawowych pojęć geometrycznych – jest rzeczą niedopuszczalną.

Jeżeli wykład Geometrji wykreślnej rozpoczynamy od ogólnej teorji rzutu środkowego, to szczegółowa analiza zagadnienia o dwukrołnem odwzorowaniu perspektywicznem elementów podstawowych: punktu, szeregu punktowego i układu płaskiego — stanowi naturalną podstawę dla teorji odpowiedniości homologicznej (Por. L. Wolfke, Wykłady Geometrji wykreślnej, tom I: „Zasady teorji perspektywy”, str. 67–110 (Warszawa, 1927).).

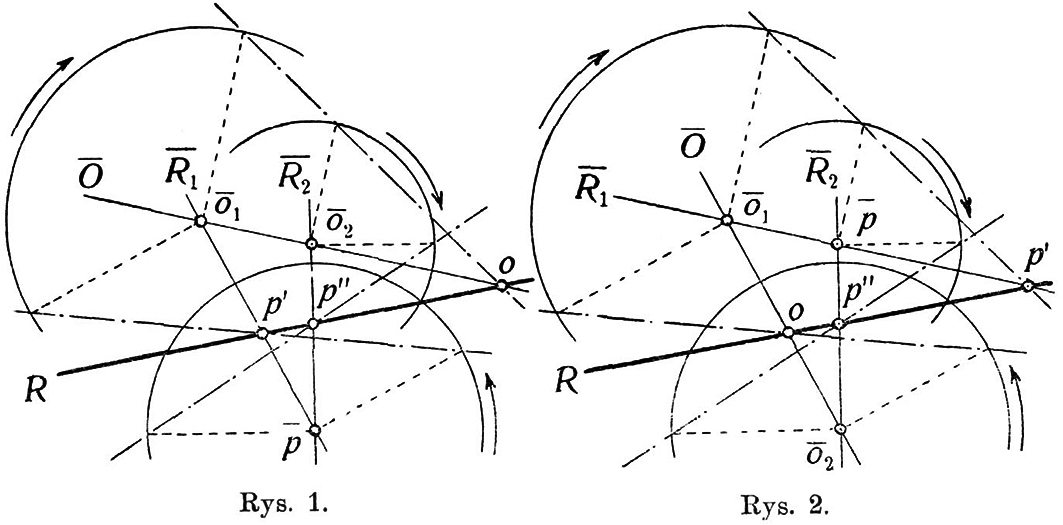
§ 1. Rzuty punktu. Posługujemy się pomocniczem odwzorowaniem cyklograﬁcznem i zakładamy, że dane są trzy różne punkty $o_{1}, o_{2}, p$ , przyczem dwa pierwsze nie leżą na płaszczyźnie rzutów $Π$ i przyjęte są za środki rzutów, a trzeci jest dowolnym punktem danym, podlegającym dwukrotnemu odwzorowaniu w rzucie środkowym (rys. 1 i 2).

Mamy wówczas trzy określone proste, a mianowicie: prostą $O$ , łączącą punkty $o_{1}$ i $o_{2}$ – czyli łącznicę środków rzutów – oraz dwie proste $R_{1}$ i $R_{2}$ łączące odpowiednio punkty $o_{1}$ i $o_{2}$ z punktem $p$ , czyli dwa promienie rzucające, poprowadzone przez punkt $p$ .

Gdy wyłączona jest współlinjowość punktów $o_{1}, o_{2}, p$ , to proste $O, R_{1}, R_{2}$ są trzema prostemi różnemi; określone jest wówczas położenie płaszczyzny $ρ$ , przesuniętej przez punkty $o_{1}, o_{2}, p$ .

Proste $O, R_{1}, R_{2}$ przebijają płaszczyznę rzutów w punktach $o, p^{'}, p^{″}$ , z których pierwszy jest śladem łącznicy środków rzutów, a dwa pozostałe stanowią, odpowiednio, pierwszy i drugi rzut punktu $p$ .

W wypadku ogólnym istnieje określona prosta $R$ : ślad płaszczyzny $ρ$ ; na takiej prostej leżą ślady trzech prostych: $O, R_{1}, R_{2}$ , należących do płaszczyzny $ρ$ .

Otrzymujemy ostatecznie następujące twierdzenia:

1.: Dwa rzuty dowolnego punktu, nie leżącego na łącznicy środków rzutów, są punktami współlinjowemi ze śladem łącznicy środków rzutów.
2.: Oba rzuty punktu, leżącego na łącznicy środków rzutów, schodzą się ze śladem tej łącznicy.
3.: Miejsce geometryczne tych punktów, z których każdy posiada rzuty zjednoczone, jest zbiorem punktowym, złożonym ze wszystkich punktów układu płaskiego i szeregu punktowego; podłożem układu jest płaszczyzna rzutów $Π$ , a podłożem szeregu jest łącznica środków rzutów $O$ .

§ 2. Rzuty prostej, wichrowatej względem łącznicy środków. Gdy rozważamy prostą $L$ , podlegającą dwukrotnemu odwzorowaniu perspektywicznemu, i zakładamy, że nie jest ona współpłaszczyznowa z łącznicą środków rzutów – z prostą $O$ , to stwierdzamy, przedewszystkiem, istnienie dwóch różnych płaszczyzn rzucających: $π_{1}$ i $π_{2}$ . Wyłączając wypadek przynależności prostej $L$ do płaszczyzny rzutów $Π$ , otrzymujemy następnie dwie nowe proste $L^{'}$ i $L^{″}$ : pierwszy i drugi rzut prostej $L$ . Proste $L, L^{'}, L^{″}$ nie leżą na jednej płaszczyźnie, są one wszakże prostemi współpunktowemi, gdyż każdy z rzutów prostej $L$ przechodzi przez jej ślad $l$ .

Zakładamy wreszcie, że prosta $L$ nie jest prostą czołową; jej ślad i oba punkty zbiegu $l_{n}^{'}$ i $l_{n}^{″}$ są wtedy punktami właściwemi. Jeżeli dane jest wówczas odwzorowanie perspektywiczne prostej $L$ , wyznaczone zapomocą środka rzutów $o_{1}$ (rys. 3), i poszukiwane jest nowe odwzorowanie prostej, to zagadnienie takie sprowadza się jedynie do wyznaczania nowego punktu zbiegu $l_{n}^{″}$ , na zasadzie jednokładności, określonej przez koła oddalenia środków rzutów; położenie śladu prostej jest, oczywiście, niezależne od położenia środka rzutów.

Gdy rozważamy proste $L, L^{'}, L^{″}$ , jako podłoża szeregów punktowych, to zapomocą dwóch pęków promieni rzucających mamy określone dwie zupełne i wzajemnie jednoznaczne odpowiedniości perspektywiczne pomiędzy szeregami punktowemi: $L$ i $L^{'}$ oraz $L$ i $L^{″}$ . Określona jest przeto w sposób pośredni pewna odpowiedniość zupełna i wzajemnie jednoznaczna pomiędzy szeregami $L^{'}$ i $L^{″}$ . Dwa rzuty każdego punktu, wziętego dowolnie na prostej $L$ , podlegają przytem twierdzeniu ogólnemu, dotyczącemu współlinjowości ze śladem łącznicy środków rzutów. Tym sposobem otrzymujemy następujące twierdzenie:

4.: Jeżeli proste $L, L^{'}, L^{″}$ są prostemi współpunktowemi, nie leżącemi na jednej płaszczyźnie, to z dwóch odpowiedniości perspektywicznych ustalonych pomiędzy szeregami punktowemi: $L$ i $L^{'}$ oraz $L$ i $L^{″}$ – wynika perspektywiczna odpowiedniość szeregów $L^{'}$ i $L^{″}$ , przyczem środek wynikowej odpowiedniości perspektywicznej jest współlinjowy ze środkami dwóch odpowiedniości danych.

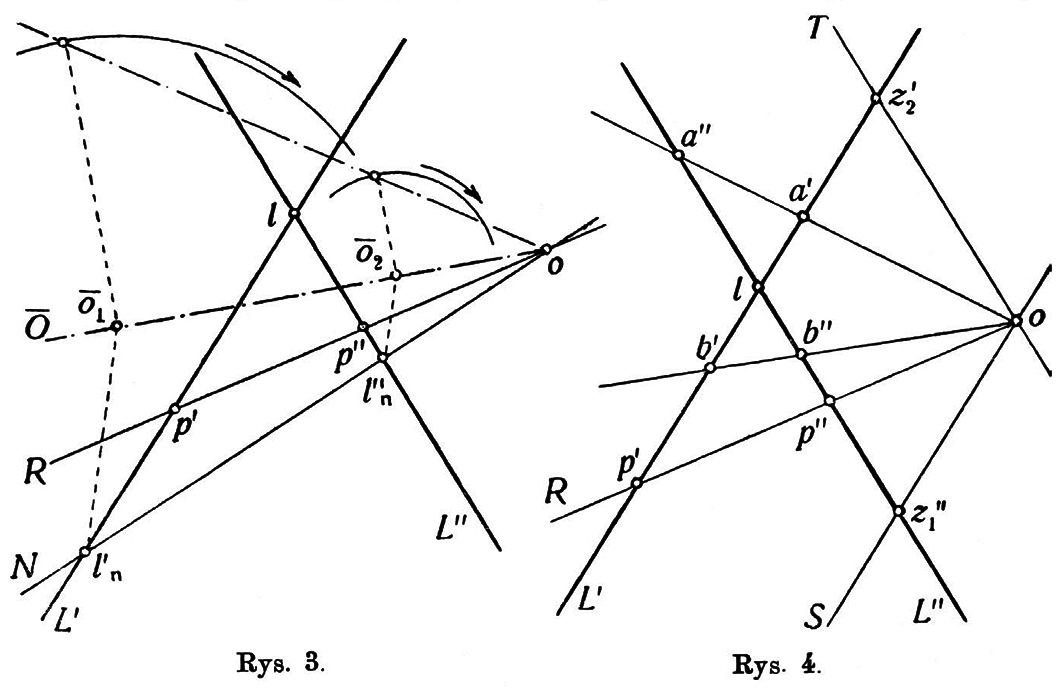
W pęku płaszczyzn, przesuniętych przez łącznicę środków; znajdujemy dwie szczególne płaszczyzny: $σ$ i $τ$ – równoległe, odpowiednio, do pierwszego i drugiego rzutu prostej $L$ ; ich punkty przecięcia z prostą daną są dwoma punktami zniknienia: $z_{1}$ i $z_{2}$ , a pozostałe, właściwe rzuty takich punktów, czyli $z_{1}^{″}$ i $z_{2}^{'}$ są dwoma punktami wzajemnemi wynikowej odpowiedniości perspektywicznej (rys. 4).

§ 3. Twierdzenia Desargues’a. Twierdzenie (4) o wynikowej odpowiedniości perspektywicznej szeregów punktowych może być również dowiedzione w tym wypadku, kiedy trzy podłoża $L^{'}, L^{″}, L^{‴}$ są prostemi współpunktowemi i jednocześnie współpłaszczyznowemi (rys. 5). Zakładamy wówczas, że dane są dwa różne punkty $o_{12}$ i $o_{22}$ – jako wierzchołki pęków, określających odpowiedniości perspektywiczne szeregów punktowych: $L^{'}$ i $L^{″}$ oraz $L^{″}$ i $L^{‴}$ .Wprowadzając dowolną prostą pomocniczą $L$ , współpunktową z podłożami rozważanych szeregów, lecz nie leżącą na ich płaszczyźnie, otrzymujemy trzy płaszczyzny różne: $π_{1}, π_{2}, π_{3}$ , przesunięte, odpowiednio, przez trzy pary prostych $L$ i $L^{'}$ , $L$ i $L^{″}$ , $L$ i $L^{‴}$ .

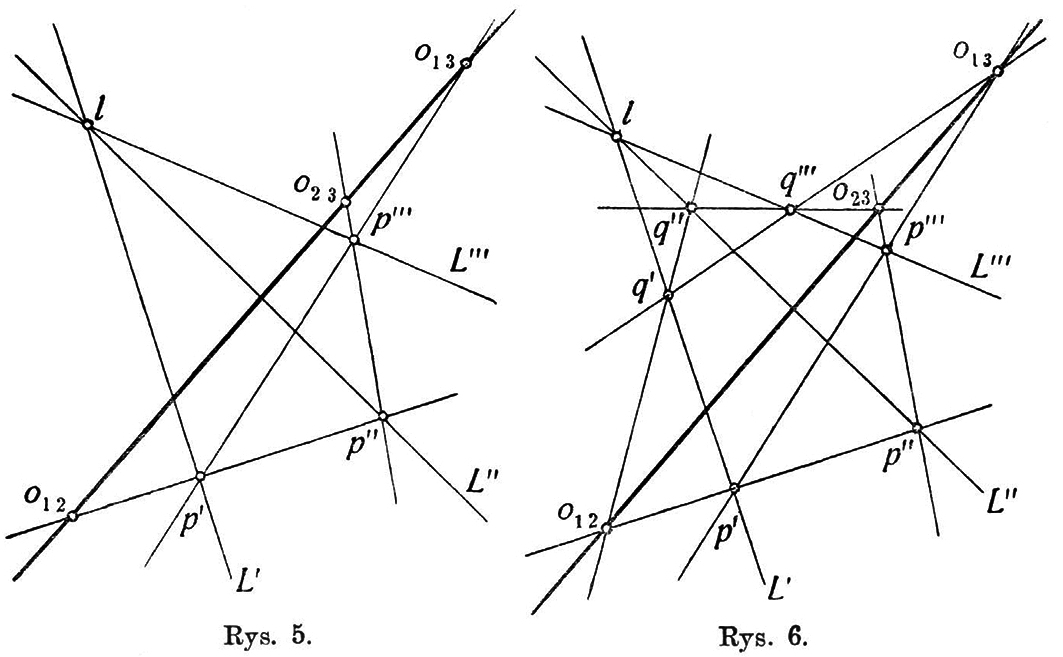
Gdy wybierzemy dowolny punkt $o_{1}$ , na płaszczyźnie $π_{1}$ i przyjmiemy go za wierzchołek pęku, określającego perspektywiczną odpowiedniość szeregów $L$ i $L^{'}$ , to podstawowe twierdzenie paragrafu poprzedniego możemy zastosować trzykrotnie, stwierdzając kolejno istnienie wynikowych odpowiedniości perspektywicznych dla następujących par szeregów punktowych:

\begin{array}{l} L i L^{″} (wierzchołek o_{2} na płaszczyźnie π_{2}), \\ L i L^{‴} (wierzchołek o_{3} na płaszczyźnie π_{3}), \\ L^{'} i L^{‴} (wierzchołek o_{13} na płaszczyźnie Π), \end{array}

Punkty $o_{1}, o_{2}, o_{3}$ są trzema punktami różnemi, gdyż leżą na trzech płaszczyznach różnych, przesuniętych przez prostą $L$ , przyczem żaden z nich nie leży na prostej $L$ .

Dwa dane punkty $o_{12}$ i $o_{22}$ , wraz z otrzymanym punktem $o_{12}$ stanowią ślady boków trójkąta $o_{1} o_{2} o_{3}$ , są więc punktami współlinjowemi.

W ten sposób otrzymujemy następujące twierdzenie:

5.: Jeżeli proste $L^{'}, L^{″}, L^{‴}$ są prostemi współpunktowemi i współpłaszczyznowemi, to z dwóch odpowiedniości perspektywicznych, ustalonych pomiędzy szeregami: $L^{'}$ i $L^{″}$ oraz $L^{″}$ i $L^{‴}$ – wynika perspektywiczna odpowiedniość szeregów $L^{'}$ i $L^{″}$ , przyczem środek wynikowej odpowiedniości perspektywicznej jest współlinjowy ze środkami dwóch odpowiedniości danych.

Opierając się na dowiedzionem twierdzeniu (5), znajdujemy punkt $o_{13}$ na łącznicy punktów $o_{12}$ i $o_{23}$ , gdy wybieramy najprzód dowolny punkt $p^{'}$ na podłożu $L^{'}$ i wykreślamy odpowiedni promień pęku $o_{13}$ po uprzedniem wyznaczeniu punktów $p^{″}$ i $p^{‴}$ na podłożach $L^{″}$ i $L^{‴}$ .

Jako wniosek z dowiedzionego twierdzenia (5), otrzymujemy twierdzenie Desargues’a, po wyznaczeniu nowej trójki punktów: $q^{'}, q^{″}, q^{‴}$ (rys. 6).

Otrzymujemy następnie dowód odwrotnego twierdzenia Desargues’a, odpowiadającego poprzedniemu na zasadzie dwoistości układu płaskiego, gdy rozważamy dwa pomocnicze trójkąty $o_{12} p^{'} q^{'}$ i $o_{23} p^{‴} q^{‴}$ .

§ 4. Rzuty szeregu współpłaszczyznowego z łącznicą środków. Zmiana środka rzutów w perspektywicznem odwzorowaniu prostej, współpłaszczyznowej z łącznicą środków, stanowi punkt wyjścia dla teorji homologji linjowej. Na wspólnej płaszczyźnie rzucającej – rozważanej w odwzorowaniu pomocniczem (rys. 7), albo w kładzie (rys. 8) – znajdujemy łącznicę środków $O$ , prostą $L$ oraz wspólne podłoże $(L^{'}, L^{″})$ dla obu rzutów szeregu punktowego $L$ .

Stwierdzamy wówczas, że ślady prostych $O$ i $L$ są dwoma punktami podwójnemi wynikowej odpowiedniości szeregów $L^{'}$ i $L^{″}$ , przyczem stała jest wartość dwustosunku czwórki punktowej $o l p^{'} p^{″}$ złożonej z punktów podwójnych i z dowolnej pary punktów odpowiednich. Dwustosunek taki, noszący nazwę cechy homologji, jest równy dwustosunkowi czwórki punktowej $o k o_{1} o_{2}$ , gdzie $k$ oznacza punkt przecięcia prostych $O$ i $L$ .

Badanie warunków przemienności homologji linjowej (warunku miarowego i warunku opisowego) doprowadza nas do twierdzenia o harmonicznych własnościach czworokąta zupełnego. Rozważając wreszcie odpowiednie punkty zniknienia i ich rzuty, stwierdzamy istnienie wspólnego środka dwóch odcinków, z których jeden łączy punkty wzajemne, a pozostały jest ograniczony przez ślady prostych $O$ i $L$ .

§ 5. Rzuty układu płaskiego. Gdy zmieniamy środek rzutów w perspektywicznem odwzorowaniu płaszczyzny $π$ , posiadającej ślad $P$ i prostą zbiegu $P_{n}^{'}$ (rys. 9), to nową prostą zbiegu $P_{n}^{″}$ wyznaczamy na zasadzie jednokładności. określonej przez koła oddalenia środków rzutów.

Do podstawowych własności opisowych, polegających na zachowaniu współlinjowości punktów i współpunktowości prostych w przekształceniu homologicznem płaskiem, jak również tych własności, które polegają na istnieniu elementów podwójnych – dołączamy następnie zasadnicze własności miarowe, dotyczące prostych wzajemnych (rys (10) i wspólnej cechy tych linjowych odpowiedniości homologicznych, które są wyznaczone na prostych, przechodzących przez ślad łącznicy środków rzutów. Opierając się na wynikach paragrafu poprzedniego, rozważamy mianowicie pęk płaszczyzn przesuniętych przez prostą O i otrzymujemy następujące twierdzenie: Homologja płaska jest zbiorem linjowych odpowiedniości homologicznych, posiadających cechę wspólną; podłoża homologji linjowych tworzą pęk promieni, którego środek jest wspólnym punktem podwójnym, a pozostałe punkty podwójne leżą na jednej prostej.